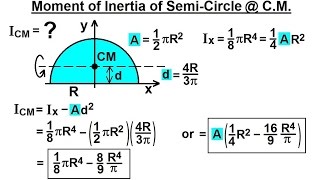
iorewlinx.blogg.se - Moment of inertia of a circle parallel axis theorem

Moment of inertia of a circle parallel axis theorem plus#

This equation is equivalent to I D 4 / 64 when we express it taking the diameter (D) of the circle. Here, R is the radius and the axis is passing through the centre. The moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of the body about the axis passing through the centre and product of the mass of the body times the square of the distance between the two axes. The word "MOI" stands for Moment of Inertia. Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression I R 4 / 4. Solve for the moment of inertia using the transfer formula. If is a point in the plane of an area and distant from the centroid of the area as shown in Fig. The parallel axis theorem also hold for the polar moment of inertia. Where is the distance between the two parallel axes. If is an axis crossing, and a parallel axis to as shown in Fig. The integral represents the moment of inertia of x- sectional area, computed about the neutral axis. Įquation 10.7 can be written for any two parallel axes with one crossing the centroid of the area.

Moment of inertia of a circle parallel axis theorem plus#

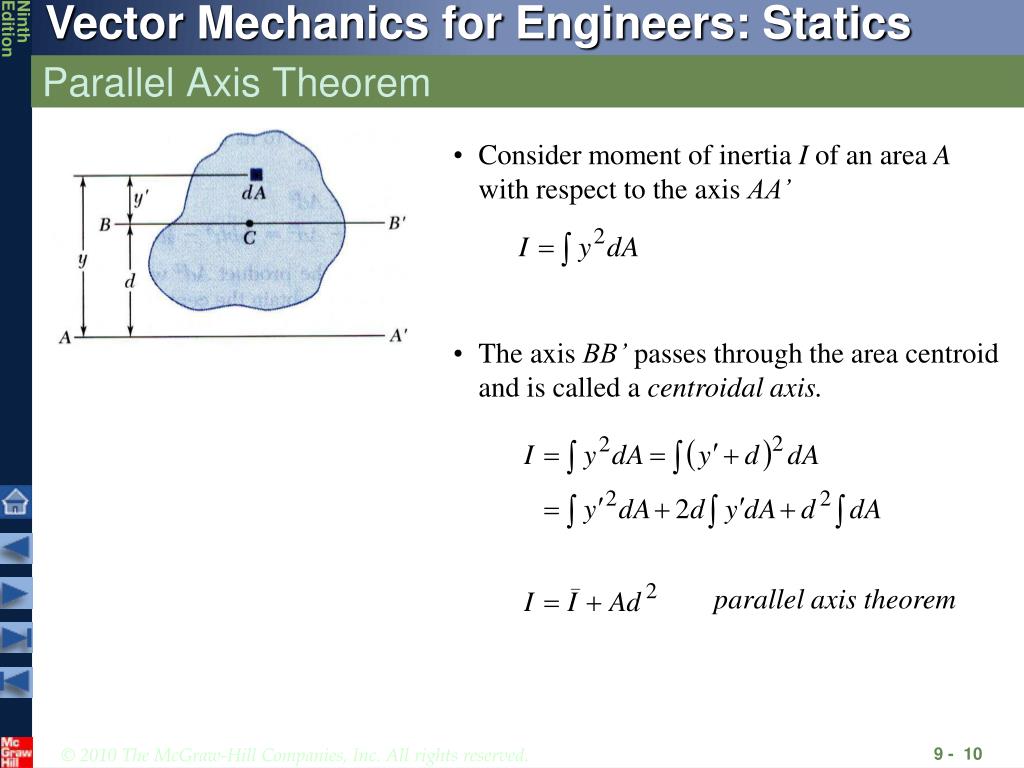
Which reads the moment of inertia about an axis is equal to the moment of inertia about a parallel axis that crosses the centroid of, plus the product of area and the square distance between and. The term equals zero because and (measured from the axis) because passes through the centroid. center 2) About tangent to the outer circle and parallel to xx axis. If is a differential element of the area, its (perpendicular) distance to the axis can be written as where is the distance between the two parallel axes shown in Fig. Find the moment of inertia of a hollow circular section having external diameter. 10.9 Terms involved in deriving the parallel axis theorem. Derivation of mass moment of inertia for.

Relationships between Load, Shear, and Momentsįig. Parallel axis theorem and perpendicular axis theorem Polar moment of inertia Mass moment of inertia.

The I-beam is 700 mmmm long and is further supported by a rod that is attached 460 mmmm from the wall. As shown, I-beam ABC supports a sign having a mass of SSS 10 kgkg.

Shear and moment equations and their diagrams To determine an I-beam’s maximum bending moment, moment of inertia using the parallel-axis theorem, and the maximum stress at a given location using the flexure formula.

Conditions for two dimensional rigid-body equilibrium.

Equilibrium of Particles and Rigid Bodies Parallel Axis Theorem The moment of area of an object about any axis parallel to the centroidal axis is the sum of MI about its centroidal axis and the prodcut of area with the square of distance of from the reference axis.

Simplification of force and couple systems.

You may need to use the parallel axis theorem to determine the Moment of Inertia of an I.

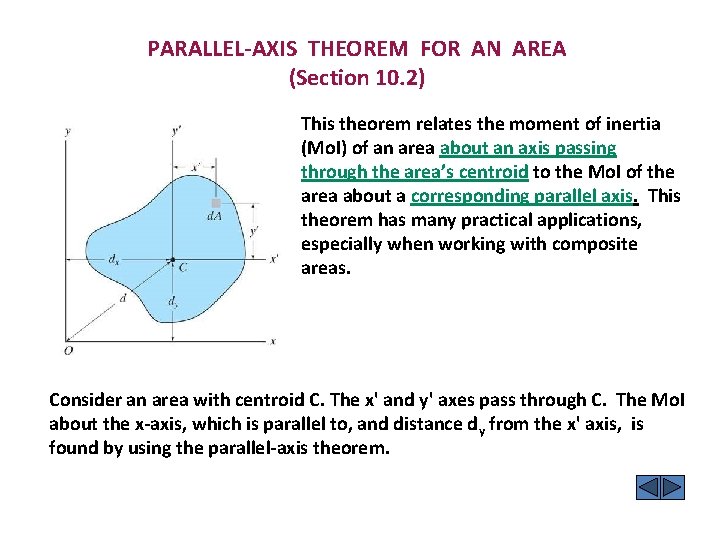
of a geometric shape can be determined by integration or the parallel-axis theorem. Oftentimes the moment of intertia of a rigid body is not taken around the centroid, rather some arbitrary point. page, Moment of Inertia of an Area page Sideway-Output on 25/11.

Vector operations using Cartesian vector notation The parallel axis theorem can be used to determine the moment of inertia of a rigid body around any axis.

IP) is given by (where, A Area of the section, IG Moment of inertia of the section about an axis passing through its C.G., and h Distance between C.G.

Vector operations using the parallelogram rule and trigonometry According to parallel axis theorem, the moment of inertia of a section about an axis parallel to the axis through center of gravity (i.e.